What Is The Don't Pass Line Bet In Craps
The term ‘dark side’ is craps parlance which is a catch-all for the Don’t Pass bet, Don’t Pass odds bets, Don’t Come bet, Don’t Come odds bet, Place-to-Lose bets, Lay Against buy bets, Don’t Pass bettor, and Don’t Come bettor. The Don’t Pass area is called the “back line” (opposite of the Pass Line, which is called the “front line”). The minimum and maximum Don’t Pass Flat bets are the same as those for the Flat Pass Line as defined on the placard located on the inside wall of the table.
'What is your opinion of betting equal amounts on the pass and don't pass lines in craps and taking full odds on the pass line? Wouldn't the pass and don't pass cancel each other out and leave only the odds, allowing me to gamble with no house edge?'
And the wizards answer is:
'No, this is not a good idea. The pass and don't pass do not cancel each other out. If you roll a 12 the pass will lose and the don't pass will push, for a net loss. To illustrate the increase in the house edge in this strategy lets assume the casino allows 5X odds. The house advantage by betting the pass line and full odds would be (7/495)/(1+5*2/3) = 0.326% . The house advantage by betting both the pass and don't pass lines and full double odds would be (7/495+27/1925)/(2+5*2/3) =0.528% . You can see the house advantage is about 62% greater by betting both the pass and don't pass lines. By adding the don't pass bet into the equation you are mixing into the formula another bet with a house advantage which brings down your overall expected return.'
My Question:
I guess I understand the math of this but not the logic. The pass bet offers two ways to win immediately, 7 or 11, and THREE ways to lose immediately, 2, 3, or 12. However the Don't Pass bet offers two ways to win immediately and ONLY TWO ways to lose yet the payout is the same. Also, if I go to the wizards Craps Appendix 2, the house edge for a pass line bet is 1.41% whereas for a Don't bet it is only 1.36%. Logically, then, the two bets combined should have a lower house edge than just the pass line bet => the average house edge would go DOWN, not UP. Since the house has no edge on the free odds bet I'm confused? Can anyone clue me into what I'm missing here?
Thanks
Stickman
PS: Also, it seems to me that by placing the Pass and the Don't Pass bets in place until a point is established, you would be reducing the overall volatility of your bankroll
the PL has EIGHT ways to win immediately and FOUR ways to lose immediately.
the DP has EIGHT ways to lose immediately and THREE ways to win immediately and ONE way to push immediately.

Yes, you do lower the volatility. In fact, if you don't put odds down, your variance will be extremely low -- you can't win.
The house edge for a doey-dont is actually the average of the two: 1/72 = 1.38889% because you lose 1 unit every 72 units bet. Some people consider this a one unit bet however because even though you have 2 units in play, only one of them will be resolved so they place the HA at 1/36 = 2.777%. When you place odds the HA does go down but by less because you have more units in play and you lose the benefit of the come out roll.
It's not a very smart bet, but it is certainly not the worst. Betting both ways is no worse than playing the field, and still not as bad as a proposition bet.
People do the same thing with a $1 bet on craps on the come out roll which pays 7:1. In a similar manner they think they are reducing their risk, because they figure that if they lose the pass line bet because the dice end up craps, at least they will win the craps bet. But it doesn't really cover you because you lose the craps bet on the 7's and 11's and all the point rolls. The house average is 11.11% if it pays 7:1 and half that if it pays 7.5:1. So it may be only a dollar bet, but the expectation is relatively low.
To get the house average of two independent bets, you simply add the house averages of the individual bets.
I proposed using this strategy and betting the PL odds for points of 6&8 and the DP odds for points other than 6 or 8, under the assumption that you'd have consistent wins. Of course the trade-off is that you are only getting small wins, while risking large bets on the DP odds.
This statement makes sense:
If you were two different people one would be playing at house advantage of 1.41% and the other would be playing at house advantage of 1.36%. So the expectation is that the two of you would lose 1.41%+1.36% of your combined money.
And, look at that:1.41 + 1.36 = 2.77 = 1/36
Go figure!
Sure, there are things like card counting that give the player an advantage. But that's a skillful way to play, not a combo of bets.
In the meantime remember three things:
1) Casinos are out to make money
2) Casinos and game makers employ people like The Wizard (sometimes they employ him specifically), to analyze their games mathematically.
3) In light of points 1 and 2, if there were a way to neutralize or reverse the HA, the casinos would get rid of it.
The rules for the various games are neither capricious nor random. They are designed to meet the casino's needs (there are exceptions, and sometimes even fascinating ones).
And, look at that: 1.41 + 1.36 = 2.77 = 1/36
Go figure!
More precisely using the fractional form you get 7/495 + 3/220 = 1/36

 Basically that is telling you that if you didn't put any 'free odds' every bet would result in a an even expected value except a 12 on the come out roll. In this case the don't pass
Basically that is telling you that if you didn't put any 'free odds' every bet would result in a an even expected value except a 12 on the come out roll. In this case the don't pass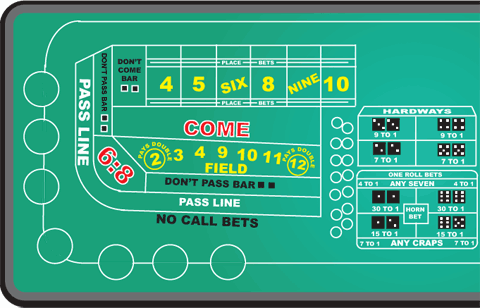 pushes, and the pass loses. This roll happens on average once out of 36 rolls.
pushes, and the pass loses. This roll happens on average once out of 36 rolls.The 'free odds' bet has no house edge.
But 1/36 > 7/495 and 1/36 > 3/220 , so you are increasing your house edge by making both bets. But you are certainly going to reduce your variance.
Like I said, it's not a smart bet, but there are much worse things you can do. A house edge of 1/36 is the normal house edge on a field bet with double 2, and triple 12.
I guess I understand the math of this but not the logic.
 I guess I understand neither. I will try to study this thread though and see if I can understand the math. I don't know if the casinos will actually let you bet both Right and Wrong though.
I guess I understand neither. I will try to study this thread though and see if I can understand the math. I don't know if the casinos will actually let you bet both Right and Wrong though.